2절 기초 통계분석
학습목표
+기술통계
- 데이터분석에서 가장 먼저 수행되는 부문
- 자료의 특성을 표, 그림, 통계량 등을 사용하에 쉽게 파악할 수 있도록 정리/요약하는 통계 분석 방법론
+기술통계를 위한 기초통계량들
- 기술통계에 활용되는 통계량은 최솟값, 최댓값, 평균, 표준편차, 분산, 중앙값, 사분위수범위, 왜도, 첨도 등
+그래프를 활용한 기술통계방법
- 막대그래프, 히스토그램, 줄기잎그림, 상자그림, 꺾은선그래프 등
+상관분석
- 두 변수 간의 관계를 분석하기 위해서 공분산과 상관계수를 활용
- 한 변수의 값이 증가할 때 상대변수의 값이 증가하면 양의상관, 상대변수의 값이 감소하면 음의상관
- 상관계술르 통해 상관성의 정도를 설명할 수 있다
1) 기술통계(Descriptive Statistics)
1. 기술통계의 정의
- 자료의 특성을 표, 그림, 통계량 등을 사용하에 쉽게 파악할 수 있도록 정리/요약하는 것
- 자료를 요약하는 기초적 통계
- 데이터 분석에 앞서 데이터의 대략적인 통계적 수치를 계산함으로써 데이터에 대한 대략적인 이해와 앞으로 분석에 대한 통찰력을 얻기에 유리
- 예 : 줄기-잎 그림, 도넛차트, 히스토그램, 상자수염그림 등
2. 통계량에 의한 자료 정리
(1) 중심위치의 측도
- 자료
- 표본평균(Sample Mean)
- 중앙값(Median)
(2) 산포의 측도
- 대표적인 산포도(Dispersion) : 분산, 표준편차, 범위 및 사분위수범위
- 분산
- 표준편차
- 사분위수범위(Interquartile Range) : IQR : Q3-Q1
- 사분위수 : 제 1사분위수(Q1)=25% / 제 2사분위수(Q2)=50% / 제 3사분위수(Q3)=75%
- 백분위수(Percentile)
- 변동계수(Coefficient of Variation)
- 표본평균의 표준오차
(3) 분포의 형태에 관한 측도
(*식까지 외울 필요는 없지만 왜도값이 주어졌을 때 어떻게 해석 하는지 알아야 합니다.
왜도가 양수인 경우엔 왼쪽으로 밀집되 어있고 오른쪽으로 긴 꼬리를 갖는 분포를 띄게 됩니다.
왜도가 음수인 경우는 오른쪽으로 밀집되어 있고 왼쪽에 긴꼬리를 갖 게 됩니다.
왜도가 0일 경우 좌우대칭의 분포를 띄게 됩니다.
*왜도의 크기에 따라 평균값(Mean)과 중앙값(Median), 최빈값 (Mode)이 변화가 있습니다.
왜도가 양수인 경우 최빈값〈중앙 값<평균 순으로 위치합니다. 왜도가 음수인 경우, 0인 경우도 체크하고 넘어갑시다!)
가) 왜도 : 분포의 비대칭정도를 나타내는 측도

나) 첨도 : 분포의 중심에서 뾰족한 정도를 나타내는 측도

3. 그래프를 이용한 자료 정리
가) 히스토그램 : 표로 되어 있는 도수 분포를 그림으로 나타낸 것으로 도수분포표를 그래프로 나타낸 것
*모자이크 플롯(Mosaic Plot): 교차표(2원, 3원)를 시각화한 그래프로 사각형들이 그래프에 나열되고 사각형의 넓이는 범주에 속한 데이터 수(또는 비율)

나) 막대그래프와 히스토그램의 비교
- 막대그래프 : 범주(Category)형으로 구분된 데이터(ex. 직업, 종교, 음식 등)를 표현하며 범주의 순서를 의도에 따라 바꿀 수 있다
- 히스토그램 : 연속(Continuous)형으로 표시된 데이터(ex. 몸무게, 성적, 연봉 등)를 표현하며 임의로 순서 바꾸기x, 막대간 간격x

다) 히스토그램 생성
- 데이터의 수를 활용해서 계급의 수와 계급간격을 계산하여 도수분포표를 만들고 히스토그램 생성
- 계급의 수 : 2^k>=n을 만족하는 최소의 정수 log2n=k에서 최소의 정수 (k는 계급 수, n은 데이터 수)
- 계급의 간격은 (최댓값-최솟값)/계급수
- 계급의 수와 간격이 변하면 히스토그램 모양이 변함
라) 줄기-잎 그림(Stem-and Leaf Plot) : 데이터를 줄기와 잎의 모양으로 그린 그림

마) 상자그림(Box Plot) : 다섯 숫자 요약(최솟값, Q1, Q2, Q3, 최댓값)을 통해 그림으로 표현
- 사분위수범위(IQR) : Q3-Q1
- 안울타리(Inner Fence) : Q1-1.5xIQR ~ Q3+1.5xIQR
- 바깥울타리(Outer Fence) : Q1-3xIQR ~ Q3+3xIQR
- 보통이상점(Mild Outlier) : 안쪽울타리와 바깥 울타리 사이 자료
- 극단이상점(Extreme Outlier) : 바깥울타리 밖의 자료


2) 인과관계의 이해
1. 용어
- 종속변수(반응변수, y) : 다른 변수의 영향을 받는 변수
- 독립변수(설명변수, x) : 영향을 주는 변수
- 산점도(Scatter Plot) : 좌표평면 위에 점들로 표현한 그래프

2. 공분산(Covariance)
- 두 확률변수 X, Y의 방향의 조합(선형성)
- 공분산의 부호만으로 두 변수 간의 방향성을 확인 가능 (+ : 양의 방향성 / - : 음의 방향성)
- X, Y가 서로 독립 : Cov(X,Y)=0 (즉, 공분산이 0 이다)
3) 상관분석(Correlation Analysis)
(1) 상관분석의 정의
- 두 변수간의 관계의 정도를 알아보기 위한 분석방법
- 두 변수의 상관관계를 알아보기 위해 상관계수(Correlation Coefficient)를 이용
(2) 상관관계의 특성

(3) 상관분석의 유형
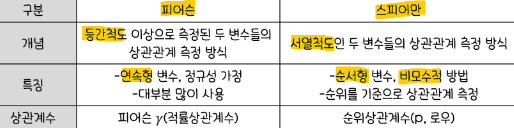
(4) 상관분석을 위한 R코드
- x: 숫자형 변수, y:NULL(default) 또는 변수, na.rm : 결측값 처리
- 분산(var) : var(x,y=NULL, na.rm=FALSE)
- 공분산(cov) : cov(x,y=NULL, use="everything", method=c("pearson","kendall","spearman"))
- 상관관계(cor/rcorr) : cor(x, y=NULL, use="everything", method=c("pearson","kendall","spearman"))
#Hmisc패키지의 rcorr사용 (상관관계)
rcorr(matrix(data명), type=c("pearson","kendall","spearman"))
rcorr(x, y, type = c("pearson", "spearman"))
(5) 상관분석의 가설 검정
- 상관계수 𝛾가 0이면 입력변수 x와 출력변수 y사이에는 아무런 관계가 없다 (귀무가설 : 𝛾=0, 대립가설 : 𝛾!=0)
- t-검정통계량을 통해 얻은 p-value 값이 0.05이하인 경우 대립가설을 채택하게 되어 우리가 데이터를 통해 구한 상관계수를 활용가능
(6) 상관분석 예제
- datasets 패키지의 mtcars라는 데이터셋의 마일(mpg), 총마력(hp)의 상관관계 분석 실시
data(mtcars)
a<-mtcars$mpg
b<-mtcars$hp
cov(a,b)
cor(a,b)
cor.test(a,b,method="pearson")
- 결과 및 해석
- mtcars 데이터셋의 mpg와 hp를 각각 a,b에 저장하여 mpg와 hp의 공분산(cov), 상관계수(cor)를 구함
- 공분산은 -320.7321, 상관계수는 -0.7761684-> mpg와 hp는 공분산으로 음의 방향성을 가짐을 알 수 있고, 상관계수로 강한 음의 상관관계가 있음을 알 수 있음
- cor.test를 이용해 상관관계 분석을 실행
> p-value가 1.788e-07로 유의수준 0.05보다 작게나타나 상관관계가 있음 -> p-value가 0.05보다 작으면 통계적으로 유의미
'ADsP(데이터 분석 준전문가) > 개념정리' 카테고리의 다른 글
| [3-4. 통계분석] 4.시계열분석 (1) | 2024.01.10 |
|---|---|
| [3-4. 통계분석] 3.회귀분석 (1) | 2024.01.10 |
| [3-4. 통계분석] 1.통계분석의 이해 (1) | 2024.01.10 |
| [3-3. 데이터 마트] 2~3. 데이터 가공 ~ 기초 분석 및 데이터 관리 (2) | 2024.01.03 |
| [3-3. 데이터 마트] 1. 데이터 변경 및 요약 (3) | 2024.01.02 |


