5장 정형 데이터 마이닝
학습목표
-데이터 마이닝의 개념
>데이터 마이닝은 기존 통계와는 달리 대용량 데이터베이스 시스템에서 데이터들 간의 의미있는 패턴을 파악하거나 예측하여 의사결정에 활용
-데이터 마이닝 방법론
> 목적에 따라서 문제를 예측하는 것과 결과를 해석하는 것으로 구분
> 종류 : 분류분석, 예측분석, 군집분석, 연관성분석 등
-데이터 마이닝 절차
> 통계분석에서 활용되는 절차와 비슷하지만 SAS에서 사용하고 있는 SEMMA방법 그리고 SPSS, 테라데이타, 다임러, NCR등에서 개발한 Crisp-DM방법
1절 데이터 마이닝의 개요
1) 데이터 마이닝
1. 개요 : 데이터 마이닝은 대용량 데이터에서 의미있는 패턴을 파악하거나 예측하여 의사결정에 활용하는 방법
2. 통계분석과의 차이점
- 통계분석은 가설이나 가정에 따른 분석이나 검증
- 데이터 마이닝은 다양한 수리 알고리즘을 이용해 데이터베이스 의 데이터로부터 의밍ㅆ는 정보를 찾아내는 방법을 통칭
3. 종류
- 정보를 찾는 방법론에 따른 종류 : 인공지능, 의사결정나무, K=평균군집, 연관분석, 회귀분석, 로짓분석, 최근접이웃법
- 분석대상, 활용목적, 표현방법에 따른 분류 : 시각화분석, 분류, 군집화, 예측
4. 사용분야
- 병원에서 환자 데이터를 이용해서 해당 환자에게 발생 가능성이 높은 병을 예측
- 기존 환자가 응급실에 왔을 때 어떤 조치를 먼저 해야 하는지를 결정
- 고객 데이터를 이용해 해당 고객의 우량/불량을 예측해 대출적격 여부 판단
- 세관검사에서 입국자의 이력과 데이터를 이용해 관세물품 반입 여부를 예측
5. 데이터 마이닝의 최근환경
- 데이터 마이닝 도구가 다양하고 체계화되어 환경에 적합한 제품을 선택하여 활용 가능하다
- 알고리즘에 대한 깊은 이해가 없어도 분석에 큰 어려움이 없다
- 분석 결과의 품질은 분석가의 경험과 역량에 따라 차이가 나기 때문에 분석과제의 복잡성이나 중요도가 높으면 풍부한 경험을 가진 전문가에게 의뢰할 필요가 있다
- 국내에서 데이터 마이닝이 적용된 시기는 1990년대 중반이다
- 2000년대에 비즈니스 관점에서 데이터 마이닝이 CRM의 중요한 요소로 부각
- 대중화를 위해 많은 시도가 있었으나, 통계학 전문가와 대기업 위주로 진행
2) 데이터 마이닝의 분석 방법
1. 지도학습
- 의사결정나무 / 인공신경망 / 일반화 선형 모형 / 선형 회귀분석 / 로지스틱 회귀분석 / 사례기반 추론 / 최근접 이웃
2. 비지도 학습
- OLAP(On-Line Analytical Processing) / 연관성 규칙 / 군집분석 / SOM(Self Organizing Map)
3) 분석목적에 따른 작업유형과 기법


4) 데이터 마이닝 추진단계
1단계 : 목적 설정
- 데이터 마이닝을 통해 무엇을 왜 하는지 명확한 목적(이해관계자 모두 동의하고 이해할 수 있는)을 설정
- 전문가가 참여해 목적에 따라 사용할 모델과 필요한 데이터를 정의
2단계 : 데이터 준비
- 고객정보, 거래정보, 상품마스터정보, 웹로그데이터, 소셜 네트워크데이터 등 다양한 데이터를 활용
- IT부서와 사전에 협의하고 일정을 조율하여 데이터 접근 부하에 유의하여야 하며, 필요시 다른 서버에 저장하여 운영에 지장이 없도록 데이터를 준비
-데이터 정제를 통해 데이터의 품질을 보장하고, 필요시 데이터를 보강하여 충분한 양의 데이터를 확보
3단계 : 가공
- 모델링 목적에 따라 목적 변수를 정의
- 필요한 데이터를 데이터 마이닝 소프트웨어에 적용할 수 있는 형식으로 가공한다
4단계 : 기법 적용
- 1단계에서 명확한 목적에 맞게 데이터 마이닝 기법을 적용하여 정보를 추출
5단계 : 검증
- 데이터 마이닝으로 추출된 정보를 검증
- 테스트 데이터와 과거 데이터를 활용하여 최적의 모델을 선정
- 검증이 완료되면 IT부서와 협의해 상시 데이터 마이닝 결과를 업무에 적용하고 보고서를 작성하여 추가수익과 투자대비성과(ROI)등으로 기대효과를 전파
5) 데이터 마이닝을 위한 데이터 분할
1. 개요 : 모델 평가용 테스트 데이터와 구축용 데이터로 분할하여, 구축용 데이터로 모형을 생성하고 테스트 데이터로 모형이 얼마나 적합한지를 판단
2. 데이터 분할
- 구축용(Training Data, 50%) : 추정용, 훈련용 데이터라고도 불리며 데이터 마이닝 모델을 만드는데 활용
- 검정용(Validation Data, 30%) : 구축된 모형의 과대추정 또는 과소추정을 미세 조정을 하는데 활용
- 시험용((Test Data, 20%)) : 테스트 데이터나 과거 데이터를 활용하여 모델의 성능을 검증하는데 활용
- 데이터의 양이 충분하지 않은 경우
가) 홀드아웃(Hold-Out) 방법 : 주어진 데이터를 랜덤하게 두개의 데이터로 구분하여 사용하는 방법으로 주로 학습용과 시험용으로 분리하여 사용
나) k-fold 교차분석(Cross-Validation) 방법
- 주어진 데이터를 k개의 하부집단으로 구분하여 k-1개의 집단을 학습용으로 나머지는 하부집단으로 검증용으로 설정하여 학습
- k번 반복 측정한 결과를 평균낸 값을 최종값으로 사용한다. 주로 10-fold 교차분석을 많이 사용한다
6) 성과분석
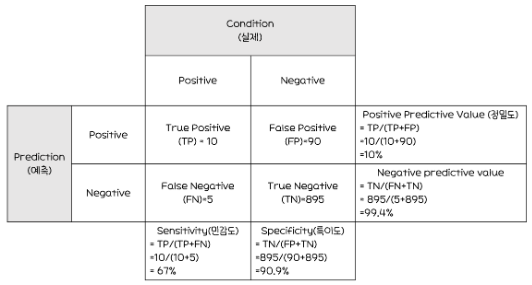
1. 오분류에 대한 추정치
사진
*코헨 카파 상관계수(Cohen's Kappa Coefficient)
- 모델의 예측값과 실제값의 일치여부를 판정하는 통계량
- 0~1사이의 범위를 가지며, 1에 가까울수록 예측-실제값 일치
*클래스 불균형(Class Imbalance)
- 분류할 각 집단에 속하는 데이터 수가 동일하지 않은 경우
- 오버 샘플링 또는 언더 샘플링 등의 해결 방안으로 처리

2. ROCR 패키지로 성과분석
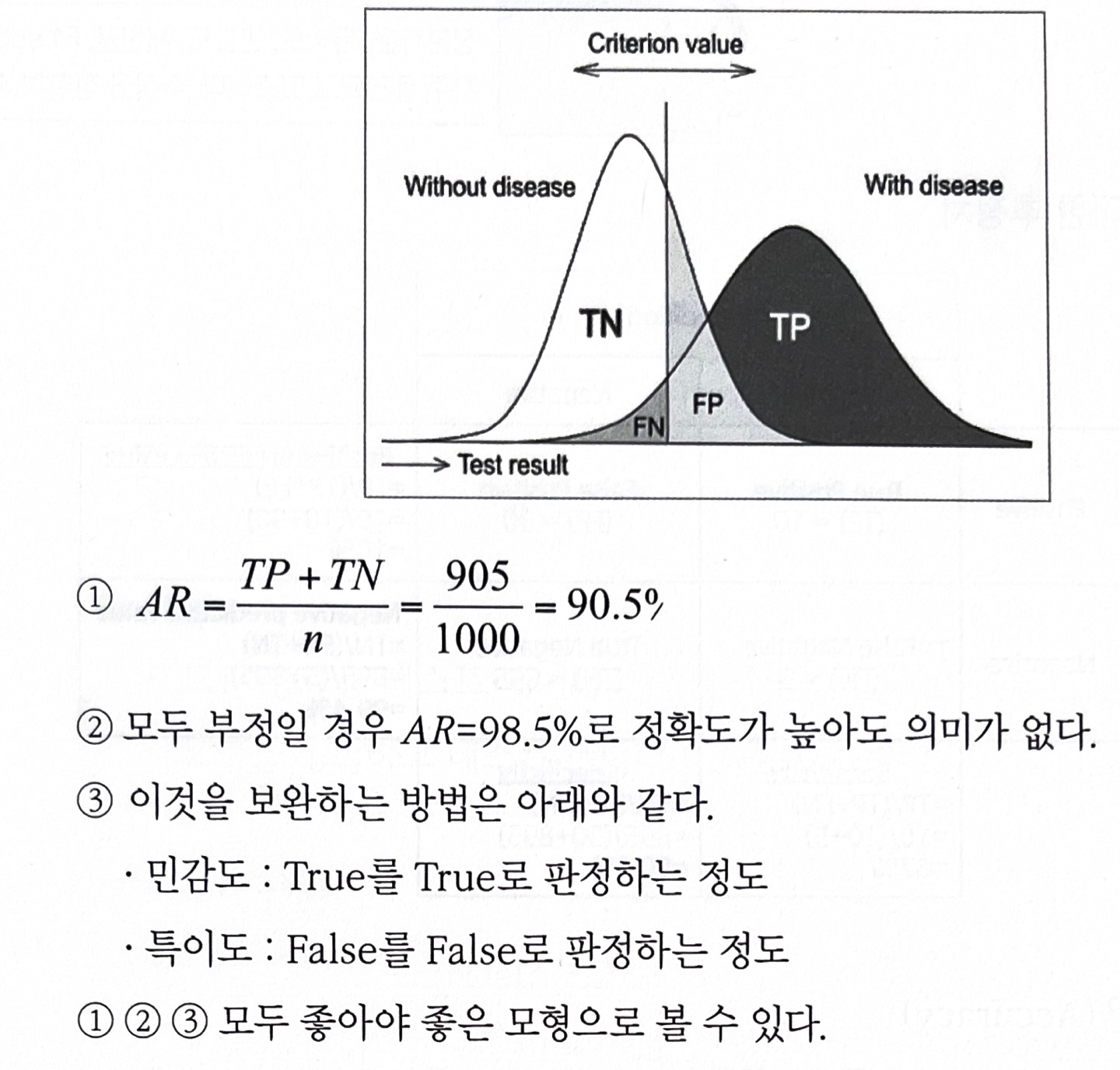
가) ROC Curve(Receiver Operating Characteristic Curve)
- ROC Curve : 가로축을 FPR(Ralse Positive Rate, 1-특이도)값으로 두고, 세로축을 TPR(True Positive Rate, 민감도)로 두어 시각화한 그래프
- 2진 분류(Binary Classfication)에서 모형의 성능을 평가하기 위해 사용되는 척도
- 그래프가 왼쪽 상단에 가깝게 그려질 수록 올바르게 예측한 비율은 높고, 잘못 예측한 비율은 낮음
- ROC곡선 아래의 면적을 의미하는 AUROC(Area Unser ROC) 값이 크면 클수록(1에 가까울 수록) 모형의 성능이 좋다고 평가
- TPR(True Positive Rate, 민감도) : 1인 케이스에 대한 1로 예측한 비율
- FPR(False Positive Rate, 1-특이도) : 0인 케이스에 대한 1로 잘못 예측한 비율
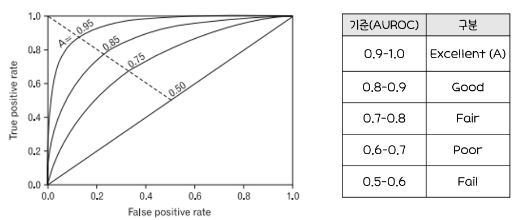
나) ROC Curve와 AUROC의 활용예시(교제 확인)
다) R 실습 코드
*sample(): 벡터혹은 데이터 프레임에서 지정된 크기만큼 데이터를 무작위로 추출할 때 사용하는 R 함수
*set.seed(): 난수를 생성하고 다시 난수를 생성하면 다른 결과가 나온다.이전과 동일한 난수를 생성하고 싶을 때 사용해 지정 가능
------------------
library(rpart)
library(party) #의사결정나무분석 포함된 패키지
library(ROCR)
#척추후만증 데이터를 nrow(kyphosis) 사이즈만큼 sample()로 무작위 추출
# replace=F로 한 번 추출한 값은 제외
x<-kyphosis[sample(1:nrow(kyphosis),nrow(kyphosis),replace=F),]
#sample()로 뽑힌 무작위 데이터 중 75%는 학습용 데이터
x.train<-kyphosis[1:floor(nrow(x)*0.75),]
#학습용 데이터 뒤부터 끝까지 평가용 (25%)
x.evaluate<-kyphosis[floor(nrow(x)*0.75):nrow(x),]
#cforest : 조건 랜덤포레스트
x.model<-cforest(Kyphosis~Age+Number+Start, data=x.train)
#x.evaluate에 없던 것을 추가. 예측
x.evaluate$prediction<-predict(x.model, newdata=x.evaluate)
x.evaluate$correct<-x.evaluate$prediction==x.evaluate$Kyphosis
print(paste("% of predicted classification correct", mean(x.evaluate$correct)))
#treeresponse는 list로 되므로 unlist 사용, probabilities는 확률
x.evaluate$probabilities<- 1-unlist(treeresponse(x.model,
newdata=x.evaluate), use.names=F)[seq(1,nrow(x.evaluate)*2,2)]
- 그래프1
#prediction(예측, 레이블(실제값))
pred<-prediction(x.evaluate$probabilities,x.evaluate$Kyphosis)
#ROC Curve를 그리기 위한 민감도, 1-특이도 계산
perf<-performance(pred, "tpr","fpr")
plot(perf, main="ROC Curve", colorize=T)
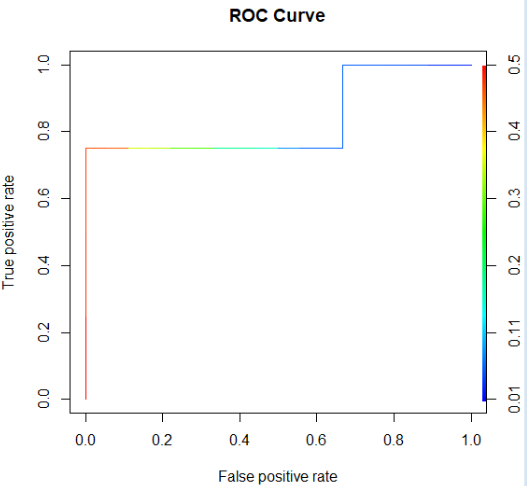
- 그래프2
# ROC 커브가 아닌 lift Curve//향상도 곡선
perf<-performance(pred,"lift","rpp")
#랜덤 모델과 비교했을 때, 해당 모델의 성과가 얼마나 향상됐는지 각 등급별로 파악
plot(perf, main="lift curve", colorize=T)
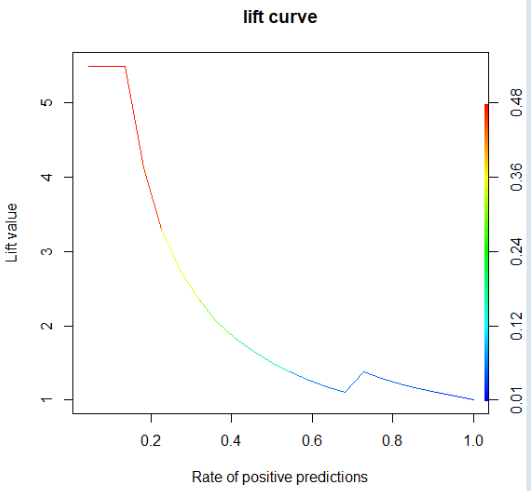
3. 이익도표(Lift chart)
가) 이익도표의 개념
- 이익도표는 분류모형의 성능을 평가하기 위한 척도로, 분류된 관측치에 대해 얼마나 예측이 잘 이루어졌는지를 나타내기 위해
임의로 나눈 각 등급별로 반응검출용, 반응률, 리프트 등의 정보를 상출하여 나타내는 도표
2000명의 전체고객 중 381명이 상품을 구매한 경우에 대해 이익도표를 만드는 과정을 예로 들어보면,
먼저 데이터셋의 각 관측치에 대한 예측확률을 내림차순으로 정렬한다
이후 데이터를 10개의 구간으로 나눈 다음 각 구간의 반응율(% response)을 산출한다
또한 기본 향상도(Baseline Lift)에 비해 반응률이 몇 배나 높은지를 계산하는데 이것을 향샹도(Lift)라고 한다
- 이익도표의 각 등급은 예측확률에 따라 매겨진 순위이기 때문에, 상위 등급에서는 더 높은 반응률을 보이는 것이 좋은 모형이라고 평가할 수 있다
나) 이익도표 활용 예시
- 전체 2000명 중 381명이 구매
- 기본 향상도(Baseline Lift) = 구매자/전체 = 381/2000
- Frequency of "buy" : 2000명 중 실제 구매자
- % Captured Response : 반응검출율=해당 등급 실구매자/전체 구매자
- % response : 반응률 = 해당 등급의 실구매자/200명(2000/10)
- Lift : 향상도 = 반응률/기본향상도, 좋은 모델이라면 Lift가 빠른 속도로 감소해야 함
- 등급별로 향상도가 급격하게 변동할수록 좋은 모형
- 각 등급별로 향상도가 들쭉날쭉하면 좋은 모형 X
참고 > 과대적합(과적합), 과소적합의 개념
*과적합/과대적합(Overfitting)
: 모형이 학습용 데이터를 과하게 학습하여, 학습 데이터에 대해서는 높은 정확도를 나타내지만, 테스트 데이터 혹은 다른 데이터에 적용할 때는 성능이 떨어지는 현상
*과소적합(Underfitting) : 모형이 너무 단순하여 데이터 속에 내제되어있는 패턴이나 규칙을 제대로 학습하지 못한 경우. 지나친 일반화
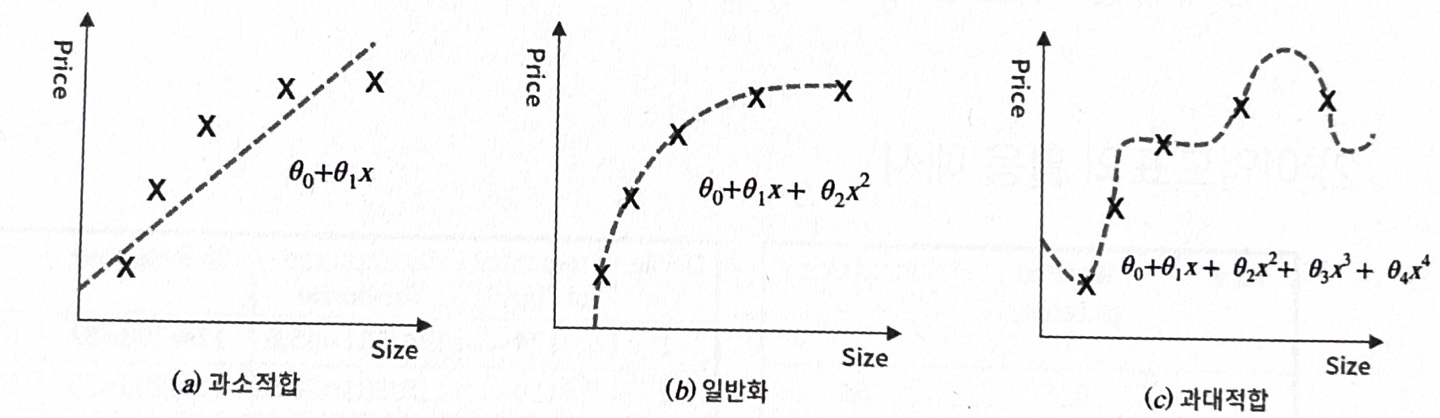
(a)과소평가:Size가 증가함에 따라 Price도 증가하는 것은 잘 표현했지만 데이터의 특징을 정확하게 설명하지 못하고 지나치게 일반화했다고 볼 수 있다
(b)일반화:데이터의 특징은 잘 설명하면서도 지나치게 학습하지 않았기 때문에 새로운 데이터를 입력하였을 때도 좋은 성능을 나타낼 수 있다
(c)과대적합:각각의 데이터를 너무 정확하게 설명하였기 때문에 새로운 데이터에 해당모형을 적용시킨다면 일반화가 힘들어 예측에 실패할 수 있다
*Bias-Variance Trade-Off
: 모델을 학습시킬 때 Bias(편향)과 Variance(분산)이 최소화가 되도록 해야지만, 하나가 커지면 하나가 작아지고 하나가 작아지면 하나가 커지기 때문에 서로 Trade-Off 관계
'ADsP(데이터 분석 준전문가) > 개념정리' 카테고리의 다른 글
| [3-5. 정형 데이터 마이닝] 3. 앙상블 분석 (0) | 2024.01.15 |
|---|---|
| [3-5. 정형 데이터 마이닝] 2.분류분석 (3) | 2024.01.15 |
| [3-4. 통계분석] 6.주성분 분석 (2) | 2024.01.10 |
| [3-4. 통계분석] 5.다차원척도법 (1) | 2024.01.10 |
| [3-4. 통계분석] 4.시계열분석 (1) | 2024.01.10 |


